|
|
|
Hydraulic Theory
Reservoir routing involves the application of the continuity equation to a storage facility in which the storage volume for a particular geometry is a dependant only on the outflow. This can be viewed as a special case of the more general kinematic wave routing procedure described in section 8.3 Kinematic Flood Routing in which the weighting coefficients are assigned values of a = 0.0 and b = 0.5 (see Figure 8.5).
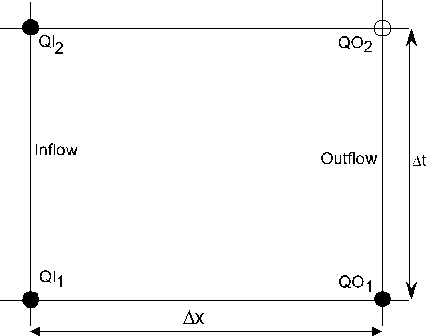
Figure 8.6 - A space-time element for reservoir routing. With reference to Figure 8.6 the continuity equation can be averaged over a time-step Dt as follows.
where QI = time series of inflow values QO = time series of outflow values S = storage volume 1,2 = subscripts corresponding to times t and t+ Dt respectively. Equation [8.46] can be expanded as follows to yield an indirect solution for the outflow QO2.
or
where
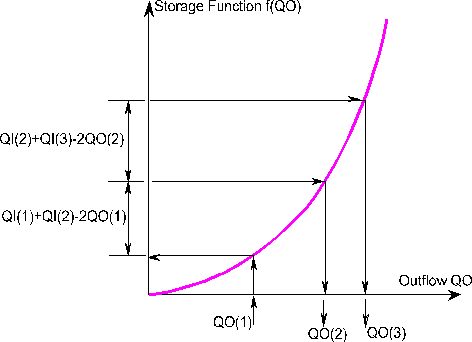
Figure 8.7 - Graphical illustration of equation [8.48]
The application of equation [8.48] is illustrated graphically in Figure 8.7. Starting with some initial, known value of QO1 = QI1 the corresponding value of f(QO1) is found by interpolation or otherwise. The inflow hydrograph QI(t) provides an upstream boundary condition from which QI2 can be found. Then from equation [8.48] a value is obtained for f(QO2) and finally by back interpolation QO2 is calculated and the process continues for other time increments. Estimating the Required Pond StorageAt the start of the Pond command MIDUSS estimates the required volume by making the assumption that the reservoir is linear. This means that the storage volume S is a linear function of the outflow QO and defined in terms of a lag coefficient K. Thus:
For this special case the storage terms can be eliminated from equation [8.47] and an explicit solution is obtained for QO2 as follows.
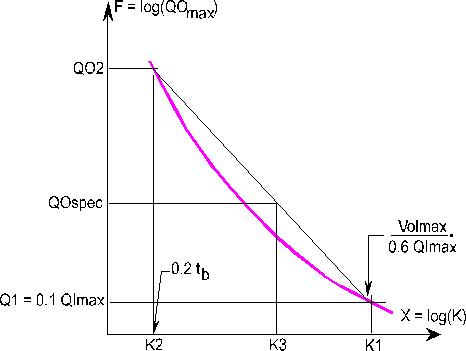
With reference to Figure 8.8, MIDUSS initially assumes that the lag coefficient K2 has a value of 0.2tb (where tb is the time base of the inflow hydrograph) and the corresponding peak outflow QO2 is obtained by applying equation [8.51] to the inflow hydrograph. Arbitrary assumptions are also made for the lag which will attenuate the peak outflow to 1/100th of the peak inflow. Using a secant method as illustrated in Figure 8.8 the estimate of K is successively improved. The relation is shown in equation [8.52].
Figure 8.8 - An iterative solution for K.
where X = log(K) F = log(QOmax) This procedure converges very rapidly on the necessary lag Kopt to produce the desired peak outflow QOspec. The corresponding storage volume is given as Sopt = Kopt x QOspec. Numerical Stability in Reservoir RoutingThe storage indication method is traditionally assumed to be inherently stable. However, this complacency is not justified in situations where the hydrograph is sharply peaked and the discharge-volume functions are poorly conditioned or exhibit pronounced discontinuities or points of contraflexure. In such circumstances, use of an arbitrary time-step can result in a computed outflow peak that is larger than the peak inflow - a condition that is physically impossible. The search for a criterion to avoid this anomaly can start with the assumption that:
Now by substituting [8.54], equation [8.49] can be written as:
or
This provides an upper limit on the routing time-step to be used which is shown in equation [8.57].
The peak outflow must lie on the recession limb of the inflow hydrograph, so that:
The routing time-step is then defined approximately as:
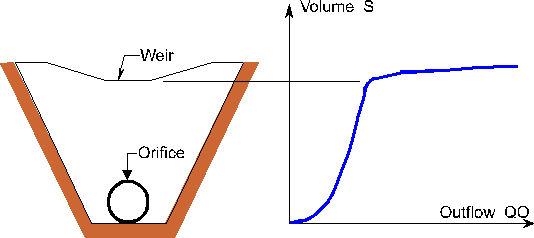
To implement this check, MIDUSS scans the storage-discharge function to determine the flattest part of the curve and uses this to determine an appropriate sub-multiple of the time-step to be used. Figure 8.9 shows a typical situation which can give rise to problems of this type.
Figure 8.9 - Storage-discharge function for a typical outlet control device.
Outflow Control Devices in PondsMIDUSS provides a number of tools to assist in the creation of the necessary table of stage, discharge and storage values which form the basis for evaluating the function f(QO) of [8.48]. This section describes how these flow estimates are made for two basic types of outflow control device. · Orifices · Weirs · Outflow pipes · Horizontal orifices Figure 8.9 shows a simple but typical device which incorporates an orifice for low flow control and a weir for less frequent flood events. Up to 10 weirs and 10 orifices can be defined. In addition, MIDUSS has a special tool to assist in the design of Rooftop Flow Control and Storage for on-site control. Orifice Flow for Pond ControlThe stage discharge equation for the orifice is calculated for two cases which depend on the relative value of the specific energy H relative to the invert of the orifice and the diameter of the orifice D. In Case 1, H > D and the orifice is fully submerged.
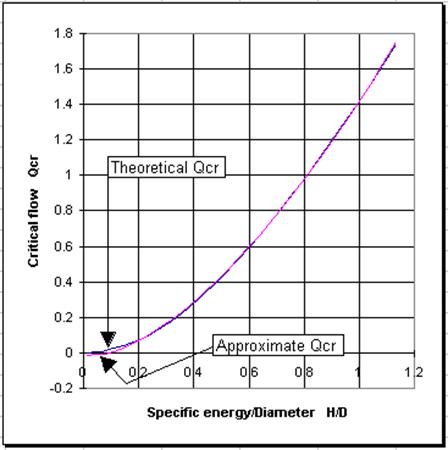
where H = head relative to the invert of the orifice D = orifice diameter g = gravitational acceleration Cc = coefficient of contraction In Case 2, H £ D and the orifice acts as a broad-crested weir of circular shape. The critical discharge can be approximated by equation [8.61]
where
Figure 8.10 - Critical flow through a segment of a circle. As shown by the comparative plot of Figure 8-10, equation [8.61] is a very reasonable approximation to the critical discharge through a segment of a circle. Weir Flow for Pond Control
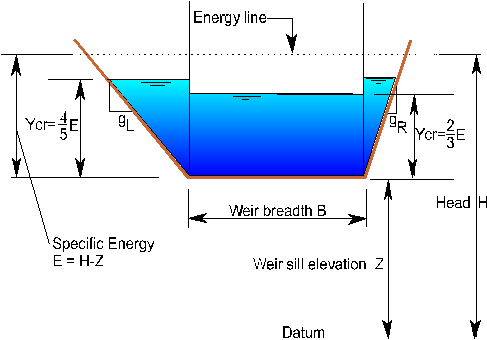
Figure 8.11 - Definition sketch of a trapezoidal weir. The weir control is assumed to have a general trapezoidal shape as illustrated above. The critical discharge is calculated for the central rectangular section and two triangular sections. For any value of head H greater than the weir sill elevation Z the critical discharge can be calculated using the general criterion for critical flow of equation [8.8]
and calculating the cross-section properties A and T in terms of the parameters shown in Figure 8.11. For a rectangular section:
where For a triangular section:
where
Typical Storage Components for Detention PondsIn addition to control flow estimation tools, MIDUSS provides a few methods for estimating the available volume in various standard storage facilities. These assist you in setting up the stage, discharge and storage values which form the basis for evaluating the function f(QO) of [8.48]. This section describes how these storage estimates are made for three basic types of storage facility. (1) Rectangular ponds (2) Super Pipes (3) Wedge (or Inverted Cone) ponding In addition, MIDUSS has a special tool to assist in the design of Rooftop Flow Control and Storage for on-site control. Rectangular Pond Storage
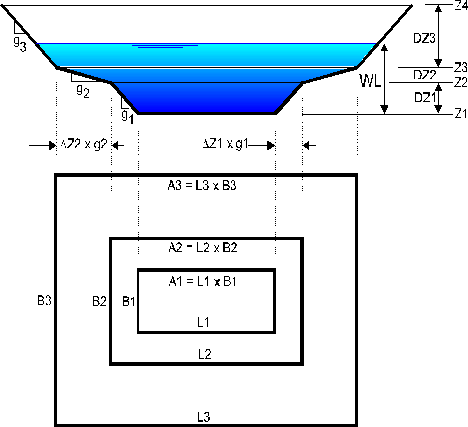
Figure 8.12 - Schematic of a 3-stage rectangular pond Detention ponds are usually constructed with side slopes which are dictated by consideration of maintenance (e.g. grass cutting) and safety. It is common for the side slope to be different at different water surface elevations. If the pond has a permanent storage component (e.g. for quality) it may be desirable to maintain a flat slope of 4:1 or 5:1 for 3m/10ft both below and above the permanent water surface elevation. Even if the pond is a "dry" pond it may be necessary to have a flatter slope at higher depths in order to get a suitably nonlinear stage-storage curve. Figure 8.12 shows an idealized pond with three stages. The shape in plan is approximated by a series of rectangles corresponding to different elevations and which have an aspect ratio L/B which reduces with increasing height. In practice it is most unlikely that the pond geometry correspond closely to this idealized shape but the rectangular pond method provides a useful design tool to estimate the general dimensions (volumes, land area etc.) required to achieve a required level of flow peak reduction. The volume is calculated using Simpson's rule so that;
where MIDUSS provides an approximate estimate for the base area A1. This is calculated from the estimate of required storage volume and assumes that only a single stage is used and that the depth is 2/3 of the depth range specified, the base aspect ratio is 2:1 and the side slope is 4H:1V. Super-Pipes for Pond Storage
Figure 8.13 - Schematic of Super Pipe Storage Figure 8.13 shows a typical arrangement of a single super-pipe with a simple outflow control device installed at the downstream end. The control can be installed either in the pipe barrel or in a manhole structure. The latter is convenient if more than one super pipe converges at a junction node. You should remember to avoid using too steep a gradient as this can seriously limit the available storage volume since the water surface is likely to be nearly horizontal. In MIDUSS the volume is obtained by calculating the cross-section of the storage at 21 equally spaced sections along the length L and then using Simpson's Rule. The section area is given as a function of the relative depth y/D from the following equations.
in which f is obtained by [8.11]
where
The volume is then obtained as:
MIDUSS provides an initial default length for a single super pipe assuming that (1) the diameter is approximately half the depth range, (2) the slope is zero (3) the pipe is full and the volume is equal to the estimated required storage. Wedges (or inverted Cones) for Pond Storage
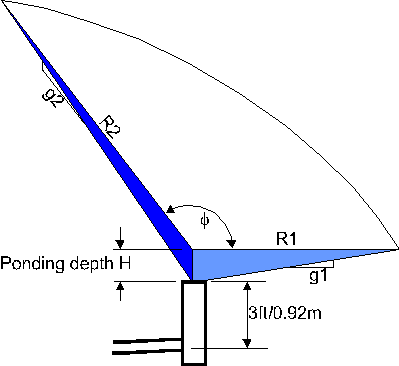
Figure 8.14 - Schematic of wedge storage To assist in
estimating the available storage on parking lots, MIDUSS provides a
wedge storage procedure that calculates the volume of a sector of a
flat, inverted cone as illustrated in Figure 8.14. The angle
subtended by the segment is defined as an angle
Figure 8.15 - Calculation of surface area of a segment of inverted, ovoid cone.
The radius R and grade g are assumed to vary linearly with the angle as shown in Figure 8.15. Then a small element of the surface area is described as:
Integrating between the limits 0 and
The volume V is then calculated as:
MIDUSS assumes that the invert of the tail pipe or the Inflow Control Device (ICD) in the catch basin is approximately 3 ft (0.92 m) below the rim elevation and that the maximum depth of ponding will probably be less than 1 ft (0.3m) above rim elevation as illustrated in Figure 8.14. To provide an initial estimate for design purposes MIDUSS assumes that the last defined impervious area has a catch basin density of 1 per 2500 sq.m or 2989 sq.yd. It is further assumed that each catch basin has a drainage area with orthogonal grades in a ratio of 2:1 (e.g. 40H:1V in one direction and 80H:1V at right angles). Based on a depth of 1 ft (0.3m) above rim elevation, the necessary grades to provide the estimated required volume are calculated and displayed together with the total number of elliptical quadrants (four such quadrants per catch basin). In setting up parking lot storage the depth range should be slightly more than 4 ft (1.22m) to comply with the assumptions made above. Rooftop Flow Control for Pond StorageFor developments involving large commercial buildings with flat roofs, on-site storage can be provided by installing roof drain controls. Typically these devices contain one or more "notches" which take the form of a linear proportional weir in which discharge is directly proportional to the head or depth of storage, for example 24 litres per minute per 25 mm of head or 6 US gallons per minute per inch of head. The actual value is defined along with other relevant parameters. If the roof is dead level then the volume of storage is calculated simply as roof area times head where the roof area available for storage is smaller (e.g. 75%) than the building footprint to allow for service structures (access, elevator, HVAC) on the roof. When a finite grade is used to promote drainage the calculation of available storage depends on whether the head H is less than or greater than the fall or difference in elevation between ridge and valley in the roof profile.
where
and L = flow length from ridge to drain S0 = roof grade
|
|||
|
|
|||
|
(c) Copyright 1984-2023 Alan A. Smith Inc. |
|
|

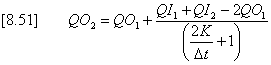
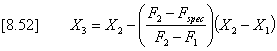
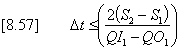
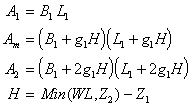

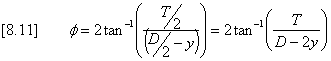

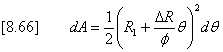 :
: