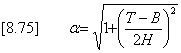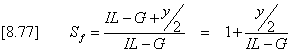Hydraulic Theory

An exfiltration trench is a facility that encourages the return of runoff to the ground water.  It may be a very simple "soak-away" and comprise only a trench filled with clear stone (i.e. single sized gravel) into which runoff is directed.  A more complex facility might be incorporated in-line with a conventional storm sewer and include one or more perforated pipes along the length of the trench to provide more uniform distribution of the inflow over the length of the trench.  It is this latter type of facility which is described in the MIDUSS Trench command. 

Figure 8.16 - A typical exfiltration trench.

Figure 8.16 illustrates a typical arrangement of an exfiltration trench which splits the inflow hydrograph into two components.  One fraction is transmitted downstream as an outflow hydrograph that is attenuated by the storage within the voids of the clear stone fill.  The balance of the flow is transmitted to the ground water through the pervious walls of the trench.  The Trench form has an option to include or exclude the base of the trench in estimating the area contributing to exfiltration.

It is usual to provide some form of outflow control device at the downstream end of the trench to force the free surface in the trench to rise.  This causes (1) the volume of voids available for storage to be increased and (2) the surface area along the walls of the trench is increased to allow increased exfiltration.  Figure 8.16 shows a typical outflow control device with a small orifice at or near the downstream invert of the trench to allow drainage of accumulated flow in the trench plus an overflow weir to produce high water levels during the maximum inflow rate.  The trench may be thought of as a variation of the "super-pipe" facility with a permeable pipe wall.

Analysis of the facility is based on a form of the continuity equation which takes account of the outflow control, the rate of exfiltration and the rate of change of storage within the trench.  Thus

                Inflow  =  Outflow + Exfiltration + Rate of change of Storage

or

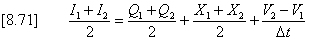
where     I              =              Inflow rate

                            Q            =              Outflow rate

                            X             =              Exfiltration rate

                            V             =              Volume stored

and the subscripts 1 and 2 define values at times  t  and  (t+Dt) respectively.

Equation [8.71] can be expanded as:

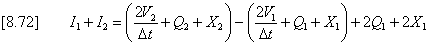
or

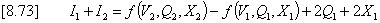
For any specified outflow control device, the water surface elevation in the trench is dependent on the outflow Q.  Both storage volume V and exfiltration X are therefore dependent on Q and a solution for the unknown outflow at time (t+Dt) can be obtained from:

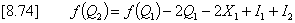
The method is similar to the graphical solution described in Figure 8.7     Graphical illustration of equation [8.48] in topic Theory of Reservoir Routing.  One difference is that it is convenient to construct curves (or tables) of both f(V,Q,X) and  X  as functions of the water surface elevation.  In order to do this we must first provide a method of predicting the rate of exfiltration from the trench.

Trench Exfiltration Rate

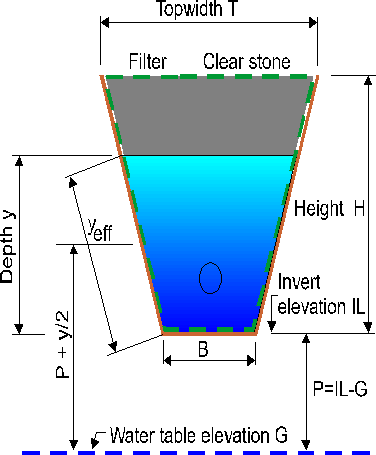
Figure 8.17 - Exfiltration Trench Cross-section

Figure 8.17 shows the cross-section assumed in MIDUSS.  The shape is a trapezium of height H and top width T tapering symmetrically to a bottom width B.  The water table is assumed to be horizontal and located at a depth P=(IL-G) below the downstream invert level of the trench.  If the depth of water in the trench voids is  y  the wetted surface of the trench wall has a length  ay  where  a  is given by:

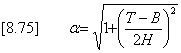
Flow through the porous soil is assumed to be laminar and can be estimated using Darcy's Law

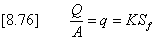
where     K             =              hydraulic conductivity of the soil

                Sf            =              friction gradient

                Q/A         =              volumetric flux.

Note that the volumetric flux is much smaller than the actual velocity through the voids since only a fraction of area A is available for flow.

The average driving head between the water in the trench and the water table is  P + y/2  and the path length is  P  so that the available gradient is given by [8.77].

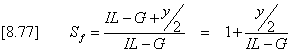
The exfiltration flow through a unit length of trench can then be estimated as:

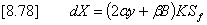
where b = 1 or 0 depending on whether the ‘Include base width’ check box is checked or unchecked.  Checked is the default condition.

Figure 8.18 - Idealized Longitudinal section on an Exfiltration Trench.

If the trench invert has a finite slope it is possible that for low flows which can be transmitted by the orifice in the outflow control device, the horizontal free surface does not extend over the full length of the trench.  Figure 8.18 shows this situation.  Even if the downstream depth is greater than the invert drop  DZ  the available surface for exfiltration must be corrected to allow for the reduced depth at the upstream end.  This assumes that the hydraulic gradient along the trench is negligible and that the surface is essentially horizontal.  The available wall surface through which exfiltration can occur is therefore given by:[8.79] and [8.80].

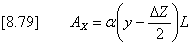                for           y³DZ

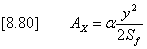                               for           y<DZ

Estimating the Required Trench Volume

When the Trench command is invoked MIDUSS tries to estimate the required trench volume (i.e. voids plus stone) which is required to achieve the currently defined target peak outflow.  The process is similar to that described in the topic Theory of Reservoir Routing; Estimating the Required Pond Storage.  However, an additional level of iteration is required as for each estimate of storage volume the corresponding exfiltration must be computed and the target outflow reduced by this amount.

As with the Pond procedure, the iteration uses the secant method to solve a relationship between Q and K to yield the required value of Q and thus estimate the storage from the corresponding lag K.

The algorithm is summarized as follows.

1.         Assume maximum exfiltration rate Xmax = 0

2.         Set desired Qout = TargetQout - Xmax

3.         Initialize values of K and Q for two points on the curve, i.e.

                            K1 = Hydrograph Volume/(0.6*Imax)

                            K2 = 0.2 Inflow hydrograph timebase

                            Q1 = 0.1 Imax

4.         Route inflow through a linear reservoir of lag K2 to get maximum outflow Q2

5.         Interpolate between points (K1,Q1) and (K2,Q2) to get K3 for required Qout

6.         For next iteration set            K1 = K2

                                                            K2 = K3

                                                            Q1 = Q2

7.         If change in Q2 > e go to step 4.

8.         Solution found for Q2.  Estimate storage  S = K2.Q2 and convert to trench volume.

9.         From trench volume estimate maximum water level Wlmax.

10.       For WL calculate exfiltration Xmax.

11.       For 5 iterations go to step 2.

Because of the many other quantities which can affect the routing operation the estimate is only an approximate guide and trial and error is normally required.

(c) Copyright 1984-2023 Alan A. Smith Inc.
Terms and Conditions       Privacy Policy