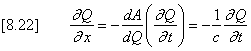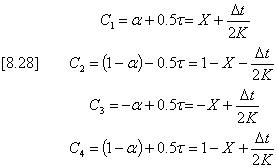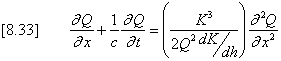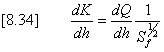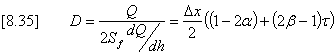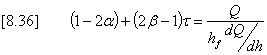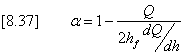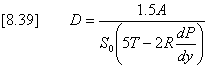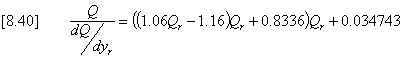|
|
|
Hydraulic Theory
Flood routing methods can be classified as hydraulic - in which both continuity and dynamic equations are used - or hydrologic, which generally uses the continuity equation alone. MIDUSS uses a method based on a kinematic wave equation and therefore falls into the second category. For the type of conduits used in storm drainage systems, kinematic routing yields results of very acceptable accuracy. The continuity equation is simply a statement that the difference between inflow and outflow must equal the rate of change of storage in the reach being considered. Equation [8.20] is a general continuity equation in which lateral inflow is ignored.
If the flow in the channel can be assumed to be quasi-uniform then discharge is uniquely defined by the depth or stage, i.e.
so that
Now separating variables in [8.20] yields:
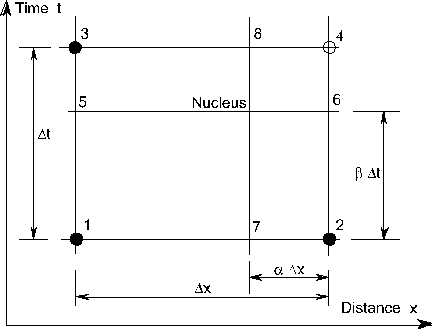
Equation [8.22] is seen to be a wave equation in which a function Q(x) is propagated with a celerity c which is given by c = dQ/dA. The variation of Q with respect to both time t and space x can be best described using a space-time coordinate system which defines changes in discharge Q in an elementary reach Dx and over a timestep Dt.
Figure 8.4 - An element of a space-time coordinate system.
Figure 8.4 shows such a situation. For this element of the space-time system equation [8.22] can be expressed in terms of finite differences as follows.
This equation is applied around a 'nucleus' of the space-time element which is off-centre and defined by the weighting factors a and b which are applied to the x and t dimensions respectively as shown in Figure 8.4. The finite difference quotients of equation [8.23] are expanded around the 'nucleus' point of Figure 8.4 in terms of the values of Q at points 5, 6, 7 & 8. These in turn can be expressed as weighted averages of the values at points 1, 2, 3 & 4 and the weighting coefficients a and b. Thus:
where Substituting equations [8.24] in [8.23] yields:
The quantity (c.Dt/Dx) is a dimensionless time ratio which is equivalent to the Courant criterion for numerical stability. Denoting this by t and substituting for Q5 etc. results in equation [8.26].
Now the process of flood routing usually involves a 'marching' solution in which the initial conditions are known at time t and it is required to predict conditions at time (t+Dt). An upstream boundary condition is provided by the time-history of the inflow hydrograph at x=0. In the case of kinematic wave routing it is possible to advance the solution for all values of time t so that the solution advances over the whole time domain for each reach of channel. In either case, the solution for the element of Figure 8.4 involves an estimate of Q4 in terms of the other three known values. Collecting terms and casting Q4 as the dependant variable yields:
where
Equation [8.27] is a generalized form of the Muskingum flood routing method but for the special case of b =0.5 this reduces to the more familiar form shown below.
Before equation [8.27] can be applied two additional pieces of information are required: (i) What values of a and b should be used to best represent the attenuation for a specific hydraulic condition? (ii) What conditions must apply for the computation to be numerically stable? Evaluation of the Weighting CoefficientsConvergence is the condition in which the solution of a finite-difference equation for a finite grid size approximates the true solution of the partial differential equation which it represents. It can be shown (Biesenthal (1975) and Smith (1980)) for the non-centred scheme of Figure 8.4 that as the coefficients a and b depart from a value of 0.5, truncation errors of the order of O(Dx) and O(Dt) increase respectively and independently. This property is fundamental to the use and apparent success of kinematic routing methods in modelling attenuation. It should be emphasized, however, that this attenuation results from truncation error and is a property of the numerical finite difference scheme and not of the physical system. The trick is to find a way to make the numerical truncation error a close approximation to the attenuation which the flood wave will experience. For a non-centred finite-difference scheme the error may be included in the partial differential equation as e in equation [8.29].
If only first order terms are included in the error term this becomes:
or
Equation [8.31] is in the form of a diffusion equation where D is the coefficient of diffusion. In order to relate D to the physical characteristics of the channel an alternate diffusion equation can be developed using the continuity equation [8.20] with a simplified form of momentum equation in which the convective and temporal accelerative terms are assumed to be negligible, i.e.
where h = water surface elevation Sf = friction gradient This can be developed (Smith(1980) see References ) to yield the diffusion equation of [8.33].
where K = channel conveyance defined by Sf = Q2/K2 Now from the definition of the conveyance K the total derivative is obtained as:
Comparison of the terms in equations [8.31] and [8.33] provides a means of evaluating the diffusion coefficient D and thus the weighting coefficients a and b in terms of the hydraulic characteristics of the channel. Thus:
where the friction head loss over the reach being considered is given by Equation [8.36] can be simplified by assuming an initial value of b = 0.5 so that:-
If equation [8.37] yields a value for a which is less than zero, MIDUSS sets a = 0.0 and solves for b from [8.36]. This value will generally be in the range 0.5 £ b £ 1.0. The generalized Muskingum coefficients of equation [8.27] can then be evaluated and a solution obtained for Q4. In MIDUSS, evaluation of the diffusion coefficient differs depending on whether the conduit is a pipe or channel. The Manning equation [8.12] can be differentiated to obtain an expression for dQ/dy as follows:
Substituting in the 2nd part of [8.35] yields an expression for D which can be evaluated in terms of the channel cross-section parameters and the channel gradient, thus:
For pipes, an alternative procedure is used in which a fitted polynomial represents the ratio Q/(dQ/dyr) as a function of the proportional discharge Qr which is the ratio of actual discharge to full pipe capacity. With very acceptable accuracy this can be represented as follows:
from which the diffusion coefficient D can be found using equation [8.35]. Criteria for Numerical Stability in Flood RoutingOnce values have been determined for the weighting coefficients a and b it is possible to carry out a check on the numerical stability of the process. This involves the calculation of limiting values for the grid dimensions Dx and Dt. Biesenthal (1975) (see References ) obtained the following condition for numerical stability.
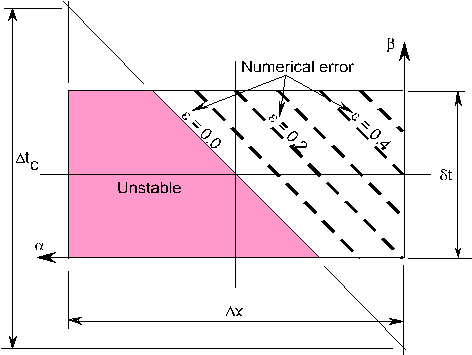
In general, this means that the nucleus of Figure 8.4 must lie above and to the right of a diagonal through the centre of the space-time element which has a slope of -(1/c).
Figure 8.5 - Stability and numerical error characteristics of a space-time element. Figure 8.5 shows a typical case in which the time step dt is approximately half of the Courant time step given by Dtc = Dx/c. The heavy dashed lines parallel to the main diagonal form a family of lines each of which comprises the locus of points for which the nucleus will generate a numerical error e of a specific value. It is significant that the same numerical attenuation can be produced by a set of ( a, b ) coordinates and MIDUSS makes use of this feature. The shaded area of Figure 8.5 indicates locations of the nucleus which are numerically unstable. Because the values of a and b are constrained to provide a required numerical error, the criterion for stability given by equation [8.38] must be satisfied by manipulating either the routing timestep dt or the reach length Dx. The greater the coarseness of the space-time grid the greater the chance of numerical instability. Thus we need to determine upper limits for both Dx and the routing time-step dt Equation [8.35] shows a relationship between the diffusion coefficient D and the weighting coefficients a and b. If we assume initially that b = 0.5 this reduces to:
Similarly if b = 0.5 the inequality [8.41] becomes:
Taking the 1st and 2nd parts of [8.43] and substituting for a from [8.42] we obtain:
or To get an upper bound for the routing time-step we use the 2nd and 3rd parts of [8.43] and obtain:
or MIDUSS uses the limiting criteria of [8.44] and [8.45] to divide either the reach length L or the hydrograph time-step ?t into sub-multiples which satisfy the conditions for stability. In the case of very long reaches the time step remains unchanged but routing is carried out over two or more subreaches. The final outflow hydrograph is the only one presented to the user. In the case of very short reaches only a single reach length is used but the routing time-step is set at d t = Dt/n (n = 2,3,4...). Only flow values at intervals of Dt are presented in the final outflow hydrograph.
|
|||
|
|
|||
|
(c) Copyright 1984-2023 Alan A. Smith Inc. |
|
|