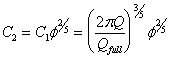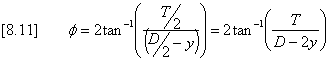|
|
|
Hydraulic Theory
This section summarizes the hydraulic principles which are used in MIDUSS for the analysis and design of pipes. Flow is assumed to be uniform within each reach of pipe, so that the depth and other cross-sectional properties are constant along the length of the pipe. It follows that the bed slope S0, the water surface and the slope of the energy line Sf are all parallel. The resistance is assumed to be represented by the Manning equation:
where Q = normal discharge (c.m/s or c.ft/s) M = 1.0 for metric units 1.49 for imperial or US customary units n = Manning's roughness coefficient A = cross-sectional area R = hydraulic radius = Area/Wetted perimeter S0 = bed slope (m/m or ft/ft) No allowance is made for any apparent variation of 'n' with the relative depth of flow in the pipe. Normal Depth in PipesFor a part-full circular section the cross-sectional properties are expressed in terms of the angle f subtended at the centre by the free surface as shown in Figure 8.1.
Figure 8.1 - Definition sketch of a part-full pipe. The following equations can be obtained by considering the geometry of the triangle subtending the half-angle f/2 at the centre of the pipe.
The value of f can be found in terms of the ratio of the discharge Q to the full-bore pipe capacity Qfull by an iterative solution of the implicit equation [8.5].
where
Equation [8.5] is solved by a Newton-Raphson procedure, thus:
where
and
Equation [8.6] is applied until Df < 0.001 radians; the depth is then determined from equation [8.7].
For a cross-section with a closed top it is usual to find that maximum normal discharge occurs at a depth slightly below full-bore flow. For a circular pipe this occurs at a relative depth of y/D = 0.93818. It follows that there must be a smaller depth which produces a discharge equal to the full-bore flow. In a part-full pipe this occurs when y/D = 0.81963. The root finding procedure in MIDUSS will always find a solution within the relative depth range 0.0 < (y/D) < 0.81963 as long as the discharge is less than the full-bore flow. If the discharge is greater than this then MIDUSS reports that the pipe will be surcharged and the slope of the hydraulic grade line is reported. (See Chapter 4 Design Options Available, Surcharged Pipe Design ) It is not possible, therefore, to take advantage of the slightly higher carrying capacity in the range 0.81963<(y/D)<1.0. It is not normally good practice to design pipes for uniform flow in this range of depth because the slightest surface disturbance will cause the free surface to 'snap through' abruptly to a condition of pressurized flow. Critical Depth in PipesWhen a pipe is designed it is often important to know if the normal flow depth y0 is less than or greater than the critical depth ycr. If y0 < ycr then the flow is supercritical and there is a high probability that a hydraulic jump will occur at some point downstream. This is usually to be avoided. The calculation of critical depth in a circular pipe is based on the critical flow condition of minimum specific energy which leads to the criterion of equation [8.8].
This is solved by an interval halving procedure using a function of the form:-
in which A is obtained by combining equation [8.3] with equations [8.10] and [8.11] below.
Convergence is assumed when Dy/y < 0.00001. Equation [8.9] cannot be solved if the free-surface width T is zero. A test is therefore made to ensure that the specified discharge is not greater than the critical discharge corresponding to a depth of ycr = 0.999 D. If this condition is violated MIDUSS assumes the critical depth to be equal to the diameter. For further information on uniform or critical flow in pipes see a text on Open Channel Flow such as Henderson (References ).
|
|||
|
|
|||
|
(c) Copyright 1984-2023 Alan A. Smith Inc. |
|
|