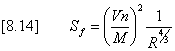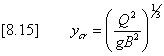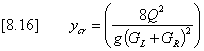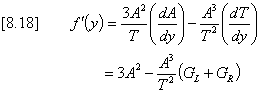Theory - Channel Design

Hydraulic Theory

Channel Design

From the MIDUSS Version 2 Reference Manual - Chapter 8
(c) Copyright Alan A. Smith Inc.

This section summarizes the methods used to analyze the channel for uniform and critical flow depth. As with the Pipe command, each reach of channel is assumed to be prismatic, that is, of constant cross-section and slope. As long as the channel flow has a free surface, the flow in each reach is assumed to be quasi-uniform, neglecting the variation of flow with time. For this condition the friction slope Sf and the water surface are assumed to be parallel to the bed slope S0. The resistance is assumed to be represented by the Manning equation [8.12].

MIDUSS lets you define the cross-sectional shape of the channel either as a trapezoidal shape as shown in Figure 8.2 or as an arbitrary cross-section defined by the coordinates of up to 50 points.

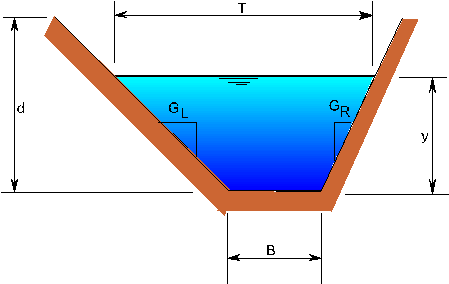
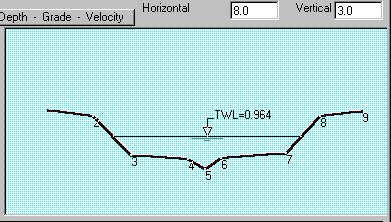
Figure 8.2 ‑ Definition of a trapezoidal section.

Figure 8.3 shows a cross-section defined by 9 points. For the purpose of illustration, the remainder of this section assumes that the cross-section is trapezoidal in shape. MIDUSS uses a simple routine to process the coordinates of a more complex section with a specified water surface elevation to yield the same cross-sectional properties.

Figure 8.3 - An arbitrary cross-section using 9 points.

Normal Depth in Channels

Figure 8.2 shows a cross-section of arbitrary trapezoidal shape, of total depth d with a flow depth y. Using the Manning equation the normal discharge Q for any given depth y is given as follows.

where Q = normal discharge (c.m/s or c.ft/s)

M = 1.0 for metric units

1.49 for imperial or US customary units (3.28 ft/m)^(1/3)

n = Manning's roughness coefficient

A = cross-sectional area

R = hydraulic radius = Area/Wetted perimeter

S0 = bed slope (m/m or ft/ft)

Evaluation of the cross-section properties depends on whether a simple trapezoidal cross-section or a more complex cross-section is defined. For a general trapezoidal shape the following equations are used.

where B = base width

T = top width

P = wetted perimeter

y = depth of flow.

GL = slope of the left bank (GL horiz : 1 vert)

GR = slope of the right bank (GR horiz : 1 vert)

and other terms are as previously defined.

The maximum carrying capacity Qfull for flow with a free surface is found from equation [8.12] setting y = d. If the peak discharge Q is less than Qfull the depth of uniform flow is found by an interval halving technique. Convergence is assumed when Dy/y < 0.000001.

The hydraulic gradient is then computed by equation [8.14].

Critical Depth in Channels

The calculation of critical depth in a channel assumes that a free surface exists. MIDUSS does not check to see if the critical depth is less than the specified total depth d.

If the base-width is finite but the side slopes are vertical the cross-section is rectangular and the critical depth can be calculated explicitly by equation [8.15].

If the basewidth is zero and at least one of the side slopes are finite the cross-section is triangular and again an explicit solution for ycr can be found from equation [8.16].

For the case of a general trapezoidal cross-section an iterative solution is required to solve the critical flow criterion of equation [8.8]. This involves the application of the Newton-Raphson method (equation [8.6]) in which the function and its derivative are defined by equations [8.17] and [8.18] respectively.

Convergence is assumed when Dy/y < 0.0001. More information on the hydraulics of open channels can be found in many standard texts (See Reference )