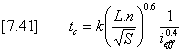Hydrological Theory

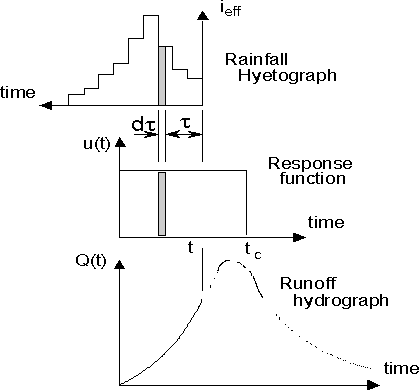
Figure 7-18 - Convolution using a rectangular response function.

Figure 7-18 illustrates a convolution process in which the response function is assumed to be rectangular with a dynamically varying time base equal to the time of concentration as defined by equation [7.41].

where    

L             =              flow length (m or feet)

n             =              Manning's roughness coefficient

S             =              slope of overland flow (m/m or ft/ft)

ieff         =              effective rainfall (mm/h or inch/h)

k             =              6.989 for metric units 

               =              0.939 for Imperial or US customary units  

The ordinate of the response function is given by umax = A/tc so that the evaluation of a discretized form of the convolution integral is relatively straightforward.  If the effective rainfall is also a simple rectangular function the method reduces to the rational method.  There is some evidence (Smith & Lee, 1984 see references) that this method is appropriate when the overland flow is dominated by runoff from relatively smooth, impervious surfaces. 

In using the Rectangular Response option it is possible to define an artificially short flowlength (e.g. 1.0 m) thus making the time of concentration of negligible duration.  This is equivalent to employing a Dirac  d‑ function as the response function and may be of interest in simulating other models.

(c) Copyright 1984-2023 Alan A. Smith Inc.
Terms and Conditions       Privacy Policy