Theory - Calculating Runoff

Hydrological Theory

Calculating Runoff

Catchment Shape

From the MIDUSS Version 2 Reference Manual - Chapter 7
(c) Copyright Alan A. Smith Inc.

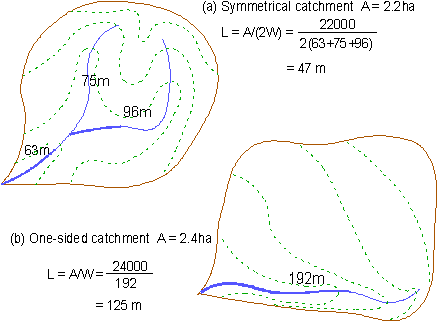
Figure 7-10 - Alternative definitions of catchment shape.

The catchment is assumed to be represented by two idealized, rectangular inclined planes - one for the pervious surface and the second for the impervious fraction. The two planes are commonly assumed to be inclined at the same gradient, but MIDUSS lets you define this and all other characteristics to be different.

For each catchment you must first specify the total catchment area and the percentage of that area which is impervious. MIDUSS then provides three options to define the shape of the two surfaces. Each of these is illustrated in a rather idealized way in Figure 7-10.

The default assumption is that the length of overland flow on the impervious surface is the same as that specified for the pervious fraction. This case is shown in Figure 7-10(a).

Alternatively, you may choose an option which assumes that the width of both rectangles is the same. This is equivalent to assuming that the overland flow lengths are in the same proportion as the areas of the two fractions, and is illustrated in Figure 7-10(b).

The third option allows you to define a specific length of overland flow for each of the two rectangles, so that neither length nor width need be the same. This case is shown in Figure 7-10(c).

From the sketches of Figure 7-10 it should be clear that the overland flow length is the distance from the boundary of the idealized rectangle to the drainage conduit (pipe or channel). It is along the overland flow length that the surface gradient should be estimated. The idealized catchments of Figure 7-10 are shown as non-symmetrical (i.e. with all the pervious or impervious area on one side of the drainage conduit) only to illustrate the concept.

In practice, it is usual for both pervious and impervious surfaces to be distributed more or less symmetrically about the drainage conduit.

Avoid the mistake of estimating overland flow length and slope between the outflow point and the point on the catchment boundary which is furthest from the outlet. This overestimates the time of concentration and underestimates the peak outflow.

If the catchment area is symmetrically distributed around the drainage network, an approximate value for the overland flow length can be found by dividing the area by twice the length of the drainage channel. If the catchment is unsymmetrical so that the drainage channel is along one edge of the catchment, the overland flow length can be approximated as (Area/Channel length). The two cases of symmetrical and one-sided catchments are illustrated in Figures 7-11(a) and (b) respectively. If neither of these cases applies then you must either make a subjective judgment or simulate the area as two separate sub-catchments.

Figure 7-11 - Estimating overland flow length in symmetrical and one-sided catchments.

Another point to note is that in MIDUSS the impervious fraction is assumed to be directly connected to the drainage network. This means that flow from the impervious areas does not pass over a pervious area before reaching the drainage channel. In some urban drainage models the impervious area is further subdivided into directly and indirectly connected fractions but these methods assume that runoff from the indirectly connected impervious area is uniformly distributed over the pervious fraction. In practice, such runoff is usually concentrated over a relatively small pervious area thus reducing the potential for infiltration. The assumption in MIDUSS therefore leads to a conservative estimate of the total runoff from the catchment.

The Manning 'n' value is used to estimate the time of concentration (see equation [7.41]) for any specific intensity of effective rainfall. Typical values of ‘n’ for overland flow on pervious surfaces should be in the range 0.2 ‑ 0.35 and do not represent realistic values of 'n' that might be used in channel flow calculations.

In addition to the above description, parameters must be defined which describe the infiltration process and rainfall abstractions on the pervious area. These will depend on the infiltration model selected and are as described in the section Calculating Effective Rainfall .