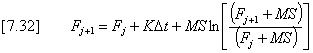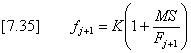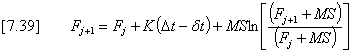Hydrological Theory

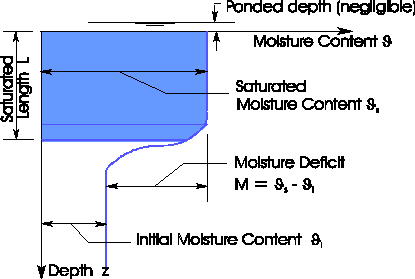
The basic assumption behind the Green and Ampt equation is that water infiltrates into (relatively) dry soil as a sharp wetting front.   Figure 7-7 below illustrates the variation in moisture content q  with depth  z  below the surface, at a point in time when the front has progressed a distance L. 

Figure 7-7 - Wetting front of the Green & Ampt model

The passage of this front causes the moisture content to increase from an initial value qi to a saturated value qs.  This difference is defined as the moisture or water deficit M, ie

Typically for dry soils M has a value in the range 0.2 < M < 0.5 depending on the soil voids ratio, with lower values for pre-wetted soil.

If the hydraulic conductivity of the soil is K (mm/hour or inches/hr) then by Darcy's law,

where    represents the hydraulic gradient.

The head causing infiltration is given by equation [7-29].

where     h0           =              depth of surface ponding (usually neglected)

                L             =              depth of water already infiltrated

                S             =              suction head at the wetting front.

The suction head S (millimetres or inches) is due to capillary attraction in the soil voids and is large for fine grained soils such as clays and small for sandy soils.

The total infiltrated volume between the surface of the soil and the wetting front is defined by equation [7-30].

The infiltration rate  f = dF/dt is then given by [7-31].

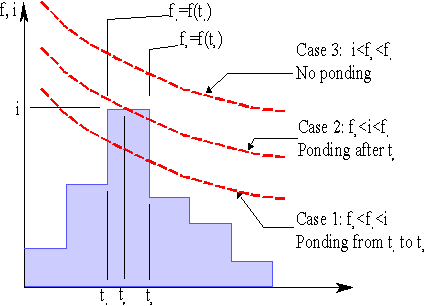
In order to calculate the effective rainfall, this equation must be solved for each time step in the storm hyetograph.  As illustrated in the Figure 7-8, three cases must be considered in which the infiltration rates at times and    are denoted by   and    respectively, and the rainfall intensity    is assumed to be constant during the time step.  Each case is considered separately.

Figure 7-8 - Three cases of the Green & Ampt model.

Case (1)                                 

i.e. the rainfall intensity exceeds the infiltration capacity of the soil throughout the whole time step so that ponding must occur for the entire time.

Case (2)                                 

i.e. at the beginning of the time step    the infiltration capacity    exceeds the rainfall intensity but this changes before the time step is completed.  Ponding will start during the time  .

Case (3)                                 

i.e. the rainfall infiltrates for the entire time step and no ponding occurs.

The solution algorithm used can be summarized as follows.

(i)            If  ij>fj  then case (1) holds and

The effective rainfall is then given by [7.33].

If  ij £ fj  then either case (2) or case (3) applies.  If we assume that case (3) applies - i.e. all the rainfall infiltrates during time  Dt - then we can estimate:

and

(iii)          Test if  i_j £ f_j+1  also.  If so, then case (3) is true and:

If  i_j > f_j+1  as computed in step (ii) then case (2) holds.  The volume required to cause surface ponding to occur is calculated as:

The time to the start of ponding  dt  can then be found from equation [7-38].

Then:

and the effective rainfall can be estimated as:-

The application of this algorithm to each time step in the storm hyetograph produces an effective rainfall hyetograph for either the impervious or pervious surface.  If the surface depression storage is finite this is subtracted from the initial elements of the hyetograph.  The remaining effective rainfall produces the direct runoff hydrograph.

In the Green and Ampt method you are prompted to supply values for a total of five parameters.  These are:

1.        Manning's 'n' roughness coefficient

2.        Water (or Moisture) deficit M (say 0.0 to 0.6)

3.        Suction head S (mm or inches)

4.        Soil conductivity K (mm/hour or inches/hour)

5.        Surface depression storage depth (mm or inches)

Parameters for the Green & Ampt equation

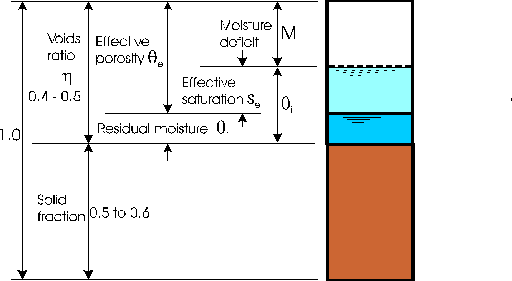
Figure 7-9 – Schematic representation of the Green & Ampt parameters

The schematic of Figure 7-9 shows the fractions of solid material, moisture and air or vapour in the soil.  The voids ratio of the soil h is typically between 0.4 to 0.5.  Within the voids of a dried sample there is a certain volume of residual moisture qr.  The remaining 'fillable' voids comprise the effective porosity  qe = h - qr and typically varies from 0.31 to 0.48.  Now if the initial moisture is denoted by  qi  the soil moisture deficit M = qe - qi .

The effective saturation is denoted by Se  = (q - qr)/ qe and can be used to estimate the suction head at the wetting front as described by Brooks and Corey, 1964. - (see references)

Some typical values suggested by Rawls, Brakensiek and Miller (1983) (see references)  are shown below.

(c) Copyright 1984-2023 Alan A. Smith Inc.
Terms and Conditions       Privacy Policy